Circuit Analysis 2

Learning Objectives Sinusoidal Waveform Phase Relations Quiz Useful Equations

Sinusoidal Waveforms

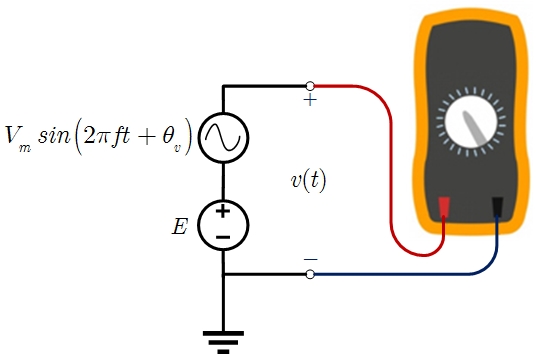
Set the variables to obtain $v (t) = 3 + 10 s i n (10 π t + 30^{\circ})$ and observe the characteristics of the waveform.

v (t) = E + V_{m} s i n (2 π f t + θ_{v})

E =

−12

V_{m} =

f =

100

θ_{v} =

degrees

−180

180

0.000

DC RMS

Click on the toggle switch of the DMM to switch between DC and RMS readings.

TIME/DIV.

10 ms

VOLT/DIV.

1 V

CH.1

1 V

CH.2

Use the knobs to adjust the time per division and volts per division.

Average Value:

V_{d c} = \frac{1}{T} \int_{0}^{T} v (t) d t = \frac{1}{T} \int_{0}^{T} [E + V_{m} s i n (2 π f t + θ_{v})] d t = E =

Effective Value:

V_{r m s} = \sqrt{V_{d c}^{2} + V_{a c (r m s)}^{2}} = \sqrt{E^{2} + (\frac{V_{m}}{\sqrt{2}})^{2}} = \sqrt{E^{2} + \frac{V_{m}^{2}}{2}} =

Peak Amplitude:

V_{m} =

Peak Value:

V_{p} = V_{m} + E =

Peak-to-peak Value:

V_{p p} = 2 V_{m} =

Instantaneous Voltage at

t_{a} =

ms:

v (t_{a}) = E + V_{m} s i n (2 π f t_{a} + θ_{v}) =