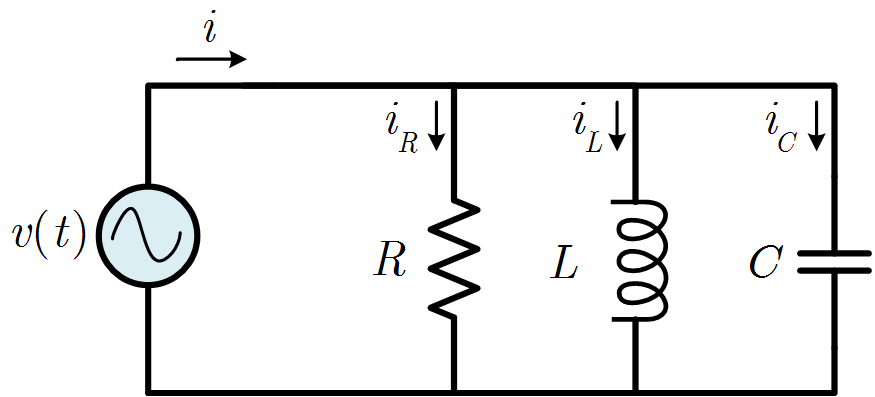
Resistor Admittance:
\( Y_R = \frac{1}{R} = \)?S
Inductor Admittance:
\( Y_L = \frac{1}{jX_L} = \frac{-j}{2\pi fL} = \)?S
Capacitor Admittance:
\( Y_C = \frac{1}{-jX_C} = j2\pi fC = \)?S
Total Admittance:
\( Y_T = Y_R+Y_L+Y_C = \)?S
Total Impedance:
\( Z_T = \frac{1}{Y_T} = \)?Ω
Input Voltage:
\( V = \frac{V_m}{\sqrt{2}}\angle \theta_v = \)
?
V
\( V_{rms} = \|V\| = \frac{V_m}{\sqrt{2}} = \)
?
V
Resistor Current:
\( I_R = \frac{V}{Z_R} = \)
?
A
\( i_R(t) = \)
?
A
Inductor Current:
\( I_L = \frac{V}{Z_L} = \)
?
A
\( i_L(t) = \)
?
A
Capacitor Current:
\( I_C = \frac{V}{Z_C} = \)
?
A
\( i_C(t) = \)
?
A
Current:
\( I = \frac{V}{Z_T} = \)
?
A
\( I_{rms} = \|I\| = \)
?
A
\( i(t) = \)
?
A
Active Power:
\( P = V_{rms}I_{rms}cos(\theta_v-\theta_i) = \)?W