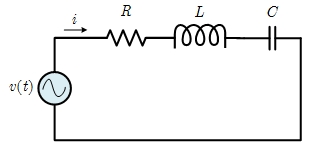
\( X_L = X_C \)
\( f_s = \frac{1}{2\pi \sqrt{LC} } \)
\( Z_{T_s} = R \)
\( Q_s = \frac{X_L}{R} = \frac{1}{R}\sqrt{\frac{L}{C}} \)
\( V_{L_s} = Q_sE \)
\( V_{C_s} = Q_sE \)
\( f_1 = \frac{1}{2\pi} \left( \frac{-R}{2L} + \frac{1}{2}\sqrt{ (\frac{R}{L})^2 + \frac{4}{LC} } \right) \)
\( f_2 = \frac{1}{2\pi} \left( \frac{R}{2L} + \frac{1}{2}\sqrt{ (\frac{R}{L})^2 + \frac{4}{LC} } \right) \)
\( BW = f_2-f_1 = \frac{R}{2\pi L} = \frac{f_s}{Q_s} \)
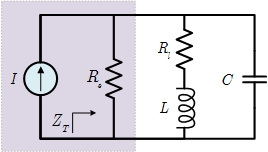
\( f_p = f_s\sqrt{1-\frac{R_l^2C}{L}} \)
\( f_m = f_s\sqrt{1-\frac{R_l^2C}{4L}} \)
\( R_p = \frac{R_l^2+X_L^2}{R_l} \)
\( Z_{T_p} = R_s || R_p \)
\( Z_{T_m} = R_s || Z_{R-L} || Z_C \)
\( Q_p = \frac{Z_{T_p}}{X_{L_p}} = \frac{Z_{T_p}}{X_C} \)
\( BW = \frac{f_p}{Q_p} \)