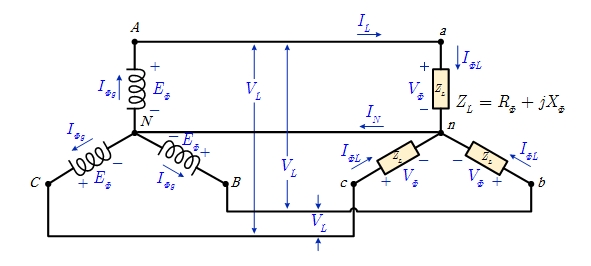
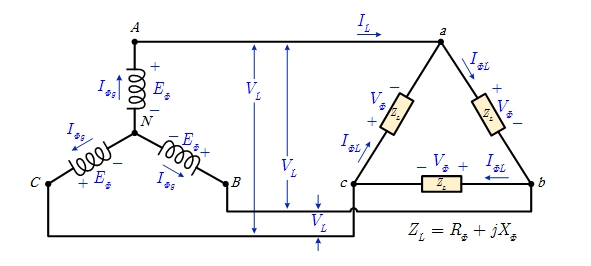
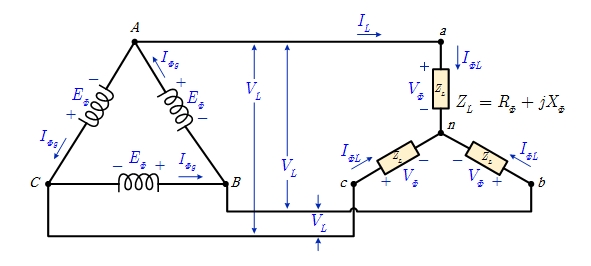
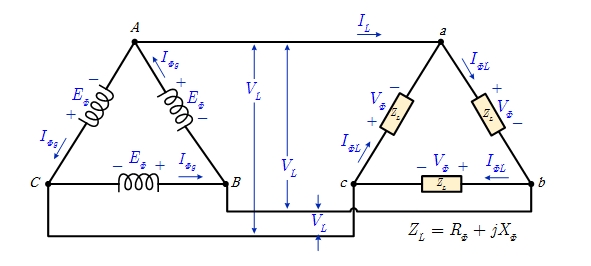
| Y-Y | Y-Δ | Δ-Y | Δ-Δ |
|---|---|---|---|
| $$ E_\Phi = \frac{V_L}{ \sqrt{3} } = V_\Phi $$ | $$ E_\Phi = \frac{V_L}{ \sqrt{3} } = \frac{V_\Phi}{ \sqrt{3} } $$ | $$ E_\Phi = V_L = \sqrt{3} V_\Phi $$ | $$ E_\Phi = V_L = V_\Phi $$ |
| $$ I_{\Phi g} = I_L = I_{\Phi L} $$ | $$ I_{\Phi g} = I_L = \sqrt{3} I_{\Phi L} $$ | $$ I_{\Phi g} = \frac{I_L}{ \sqrt{3} } = \frac{I_{\Phi L}}{ \sqrt{3} }$$ | $$ I_{\Phi g} = \frac{I_L}{ \sqrt{3} } = I_{\Phi L} $$ |
 |
 |
 |
 |
Active Power: $$ P_\Phi = V_\Phi I_{\Phi L} cos\theta_{I_{\Phi L}}^{V_\Phi} = I_{\Phi L}^2 R_\Phi = \frac{V_R^2}{R_\Phi} $$ $$ P_T = 3P_\Phi $$
Reactive Power: $$ Q_\Phi = V_\Phi I_{\Phi L} sin\theta_{I_{\Phi L}}^{V_\Phi} = I_{\Phi L}^2 X_\Phi = \frac{V_X^2}{X_\Phi} $$ $$ Q_T = 3Q_\Phi $$
Apparent Power: $$ S_\Phi = V_\Phi I_{\Phi L} $$ $$ S_T = 3S_\Phi = \sqrt{3}E_L I_L $$
Power Factor: $$ F_P = \frac{P_T}{S_T} $$